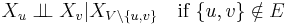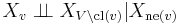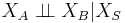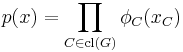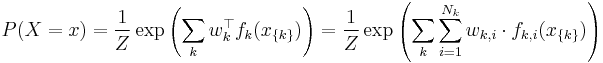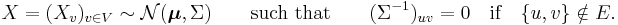Markov random field
A Markov random field, Markov network or undirected graphical model is a set of random variables having a Markov property described by an undirected graph. It is also referred to as a Gibbs random field in case the probability distribution is positive, because, according to the Hammersley–Clifford theorem, it can then be represented by a Gibbs measure. A Markov random field is similar to a Bayesian network in its representation of dependencies. It can represent certain dependencies that a Bayesian network cannot (such as cyclic dependencies); on the other hand, it can't represent certain dependencies that a Bayesian network can (such as induced dependencies). The prototypical Markov random field is the Ising model; indeed, the Markov random field was introduced as the general setting for the Ising model[1]. A Markov random field is used to model various low- to mid-level tasks in image processing and computer vision.[2] For example, MRFs are used for image restoration, image completion, segmentation, texture synthesis, super-resolution and stereo matching.
Contents |
Definition
Given an undirected graph G = (V, E), a set of random variables X = (Xv)v ∈ V indexed by V form a Markov random field with respect to G if they satisfy the following equivalent Markov properties:
- Pairwise Markov property: Any two non-adjacent variables are conditionally independent given all other variables:
- Local Markov property: A variable is conditionally independent of all other variables given its neighbours:
-
- where ne(v) is the set of neighbours of v, and cl(v) = {v} ∪ ne(v) is the closed neighbourhood of v.
- Global Markov property: Any two subsets of variables are conditionally independent given a separating subset:
-
- where every path from a node in A to a node in B passes through S.
Clique factorization
As the Markov properties of an arbitrary probability distribution can be difficult to establish, a commonly used class of Markov random fields are those that can be factorized according to the cliques of the graph.
Given a set of random variables X = (Xv)v ∈ V for which the joint density (with respect to a product measure) can be factorized over the cliques of G:
then X forms a Markov random field with respect to G, where cl(G) is the set of cliques of G (the definition is equivalent if only maximal cliques are used). The functions φC are often referred to as factor potentials or clique potentials.
Although some MRFs do not factorize (a simple example can be constructed on a cycle of 4 nodes[3]), in certain cases they can be shown to be equivalent conditions:
- if the density is positive (by the Hammersley–Clifford theorem),
- if the graph is chordal (by equivalence to a Bayesian network).
When such a factorization does exist, it is possible to construct a factor graph for the network.
Examples
Log-linear models
A log-linear model is a Markov random field with feature functions 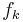 such that the full-joint distribution can be written as
such that the full-joint distribution can be written as
with partition function
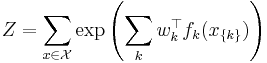 .
.
where 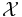 is the set of possible assignments of values to all the network's random variables. Usually, the feature functions
is the set of possible assignments of values to all the network's random variables. Usually, the feature functions 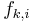 are defined such that they are indicators of the clique's configuration, i.e.
are defined such that they are indicators of the clique's configuration, i.e. 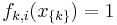 if
if 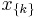 corresponds to the i-th possible configuration of the k-th clique and 0 otherwise. This model is thus equivalent to the general formulation above if
corresponds to the i-th possible configuration of the k-th clique and 0 otherwise. This model is thus equivalent to the general formulation above if 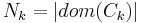 and the weight of a feature
and the weight of a feature 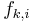 corresponds to the logarithm of the corresponding clique potential, i.e.
corresponds to the logarithm of the corresponding clique potential, i.e. 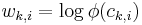 , where
, where 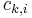 is the i-th possible configuration of the k-th clique, i.e. the i-th value in the domain of the clique
is the i-th possible configuration of the k-th clique, i.e. the i-th value in the domain of the clique 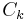 . Note that this is only possible if all clique potentials are non-zero, i.e. if none of the elements of
. Note that this is only possible if all clique potentials are non-zero, i.e. if none of the elements of 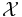 are assigned a probability of 0.
are assigned a probability of 0.
Log-linear models are especially convenient for their interpretation. A log-linear model can provide a much more compact representation for many distributions, especially when variables have large domains. They are convenient too because their negative log likelihoods are convex. Unfortunately, though the likelihood of a log-linear Markov network is convex, evaluating the likelihood or gradient of the likelihood of a model requires inference in the model, which is in general computationally infeasible.
Gaussian Markov random field
A multivariate normal distribution forms a Markov random field with respect to a graph G = (V, E) if the missing edges correspond to zeros on the precision matrix (the inverse covariance matrix):
Inference
As in a Bayesian network, one may calculate the conditional distribution of a set of nodes 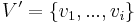 given values to another set of nodes
given values to another set of nodes 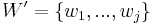 in the Markov random field by summing over all possible assignments to
in the Markov random field by summing over all possible assignments to 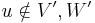 ; this is called exact inference. However, exact inference is a #P-complete problem, and thus computationally intractable in the general case. Approximation techniques such as Markov chain Monte Carlo and loopy belief propagation are often more feasible in practice. Some particular subclasses of MRFs, such as trees see Chow-Liu tree, have polynomial-time inference algorithms; discovering such subclasses is an active research topic. There are also subclasses of MRFs that permit efficient MAP, or most likely assignment, inference; examples of these include associative networks.
; this is called exact inference. However, exact inference is a #P-complete problem, and thus computationally intractable in the general case. Approximation techniques such as Markov chain Monte Carlo and loopy belief propagation are often more feasible in practice. Some particular subclasses of MRFs, such as trees see Chow-Liu tree, have polynomial-time inference algorithms; discovering such subclasses is an active research topic. There are also subclasses of MRFs that permit efficient MAP, or most likely assignment, inference; examples of these include associative networks.
Conditional random fields
One notable variant of a Markov random field is a conditional random field, in which each random variable may also be conditioned upon a set of global observations 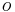 . In this model, each function
. In this model, each function 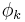 is a mapping from all assignments to both the clique k and the observations
is a mapping from all assignments to both the clique k and the observations 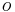 to the nonnegative real numbers. This form of the Markov network may be more appropriate for producing discriminative classifiers, which do not model the distribution over the observations.
to the nonnegative real numbers. This form of the Markov network may be more appropriate for producing discriminative classifiers, which do not model the distribution over the observations.
See also
- Maximum entropy method
- Hopfield network
- Graphical model
- Markov chain
- Markov logic network
- Hammersley–Clifford theorem
- Markov-Gibbs properties
References
- ^ Kindermann, Ross; Snell, J. Laurie (1980). Markov Random Fields and Their Applications. American Mathematical Society. ISBN 0-8218-5001-6. MR0620955. http://www.ams.org/online_bks/conm1/.
- ^ Li, S. Z. (2009). Markov Random Field Modeling in Image Analysis. Springer.
- ^ Moussouris, John (1974). "Gibbs and Markov random systems with constraints". Journal of Statistical Physics 10 (1): 11–33. doi:10.1007/BF01011714. MR0432132.
- ^ Rue, Håvard; Held, Leonhard (2005). Gaussian Markov random fields: theory and applications. CRC Press. ISBN 1584884320.